Forecasting realized volatility using IV, Overnight Returns and Leverage Effect
We use exegenous variables to improve the predictive power of a HAR model.
This post was inspired by the following paper:
https://onlinelibrary.wiley.com/doi/epdf/10.1002/fut.22241
Libraries
Pandas, Numpy, Matplotlib, Sklearn and math are used.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
import mathData
We use daily SPY and VIX data from 01/01/2000 to 06/27/2023
VIX will be used as our measure of IV.
HAR Model
The paper uses a HAR model and builds on top of it.
The intuition behind the model is quite simple:
Different market participants react to different time horizons differently, because of this we use historical daily, weekly and monthly variance in model to predict next days variance.
Our Model looks like this:
RV stands for our realized variance, RV^d is daily variance, RV^w is weekly variance and RV^m is monthly variance, the alphas are our model coefficients.
We are gonna use past 1 day for daily, past 5 days for weekly and past 22 days for monthly.
We can get our coefficients using simple multiple regression.
The paper defines RV as the sum of squared intraday returns. We are gonna use the sum of squared daily returns.
SPY['rets'] = ((SPY['Close']-SPY['Close'].shift(1))/SPY['Close'].shift(1)).fillna(0)
SPY['RV_d'] = SPY['rets']**2
SPY['RV_w'] = SPY['RV_d'].rolling(window=5).sum()
SPY['RV_m'] = SPY['RV_d'].rolling(window=22).sum()regr = linear_model.LinearRegression()
regr.fit(SPY[['RV_d', 'RV_w', 'RV_m']][22:-1], SPY['RV_d'][23:])
coefs = regr.coef_
intercept = regr.intercept_Let’s try out our model!
SPY['RV_d_pred'] = intercept + coefs[0]*SPY['RV_d'] + coefs[1]*SPY['RV_w'] + coefs[2]*SPY['RV_m']It’s not perfect but looks like we are going in the right direction.
The paper actually does 1 small change, it looks at the logarithm of the Realized Volatility because that brings the distribution closer to normal, we are gonna continue using regular RV though.
Let’s look at our prediction error:
error = SPY['RV_d_pred']-SPY['RV_d']The paper uses some really complicated evaluation methods to determine how good the models are, we are gonna use something simpler: the sum of squared errors.
Which for this model is the following: 0.0013392886731592585
Adding additional exegenous variables
We can add as many more new variables as we want and try to improve our model that way. We are gonna be using IV in the form of VIX, overnight returns and leverage effect.
Generalized we will have a vector X of exegenous variables and a vector beta of our coefficients. Our new model becomes:
Let’s start off with overnight returns:
SPY['overnight_rets'] = ((SPY['Open']-SPY['Close'].shift(1))/SPY['Close'].shift(1)).shift(-1).fillna(0)regr_overnight = linear_model.LinearRegression()
regr_overnight.fit(SPY[['RV_d', 'RV_w', 'RV_m', 'overnight_rets']][22:-1], SPY['RV_d'][23:])
coefs_overnight = regr_overnight.coef_
intercept_overnight = regr_overnight.intercept_SPY['RV_d_pred_overnight'] = intercept_overnight + coefs_overnight[0]*SPY['RV_d'] + coefs_overnight[1]*SPY['RV_w'] + coefs_overnight[2]*SPY['RV_m'] + coefs_overnight[3]*SPY['overnight_rets']error_overnight = SPY['RV_d_pred_overnight']-SPY['RV_d']The new error metric becomes: 0.0013392905716341152
Doesn’t look like that improved anything, let’s try the leverage effect.
The leverage effect refers to the fact that high volatility usually comes with negative returns. Let’s add positive and negative returns to our model and see if it picks up on this effect.
SPY['pos_rets'] = SPY['rets'].apply(lambda x: x if x > 0 else 0)
SPY['neg_rets'] = SPY['rets'].apply(lambda x: x if x < 0 else 0)regr_leverage = linear_model.LinearRegression()
regr_leverage.fit(SPY[['RV_d', 'RV_w', 'RV_m', 'pos_rets', 'neg_rets']][22:-1], SPY['RV_d'][23:])
coefs_leverage = regr_leverage.coef_
intercept_leverage = regr_leverage.intercept_SPY['RV_d_pred_leverage'] = intercept_leverage + coefs_leverage[0]*SPY['RV_d'] + coefs_leverage[1]*SPY['RV_w'] + coefs_leverage[2]*SPY['RV_m'] + coefs_leverage[3]*SPY['pos_rets'] + coefs_leverage[4]*SPY['neg_rets']error_leverage = SPY['RV_d_pred_leverage']-SPY['RV_d']Our new error metric becomes: 0.0013630858070074444
Still no improvements.
Let’s look at our final exegenous variable: IV
SPY['IV'] = VIX['Close'].fillna(0)regr_iv = linear_model.LinearRegression()
regr_iv.fit(SPY[['RV_d', 'RV_w', 'RV_m', 'IV']][22:-1], SPY['RV_d'][23:])
coefs_iv = regr_iv.coef_
intercept_iv = regr_iv.intercept_SPY['RV_d_pred_iv'] = intercept_iv + coefs_iv[0]*SPY['RV_d'] + coefs_iv[1]*SPY['RV_w'] + coefs_iv[2]*SPY['RV_m'] + coefs_iv[3]*SPY['IV']error_iv = SPY['RV_d_pred_iv']-SPY['RV_d']Our new error metric becomes: 0.0013557585821825549
Let’s try combining all of our exegenous variables in a last test.
regr_all= linear_model.LinearRegression()
regr_all.fit(SPY[['RV_d', 'RV_w', 'RV_m', 'overnight_rets', 'pos_rets', 'neg_rets', 'IV']][22:-1], SPY['RV_d'][23:])
coefs_all = regr_all.coef_
intercept_all = regr_all.intercept_SPY['RV_d_pred_all'] = intercept_iv + coefs_iv[0]*SPY['RV_d'] + coefs_iv[1]*SPY['RV_w'] + coefs_iv[2]*SPY['RV_m'] + coefs_iv[3]*SPY['overnight_rets'] + coefs_iv[4]*SPY['pos_rets'] + coefs_iv[5]*SPY['neg_rets'] + coefs_iv[6]*SPY['IV']error_all = SPY['RV_d_pred_all']-SPY['RV_d']And the final error metric becomes: 0.0013639558982212283
What went wrong?
Let’s plot all of our predictions to answer that:
Notice anything? All of our predictions basically perfectly overlap.
In other words even though our exegenous variables may be predictive of future variance they don’t bring in any new useful information that isn’t already contained in our historical RVs.
So instead of trying to just add new exegenous variables let’s modify our model directly. Let’s start with leverage effect:
Our new model is gonna look like this:
So if our our last return was positive we don’t change our prediction.
If our last return was negative we scale with the squared return.
So step 1 is to fit the model as usual which we have already done.
For step 2 we are just gonna try out a bunch of different values for now and see which one works best for now. This is obviously not an optimal method but it will show us if our idea works.
beta_arr = []
error_arr = []
for beta in np.arange(1, 1000, 1):
beta_arr.append(beta)
SPY['RV_d_pred_modified'] = SPY['RV_d_pred']
for i in range(1, len(SPY)):
if SPY['rets'][i] < 0:
SPY['RV_d_pred_modified'][i] *= beta*SPY['rets'][i]**2
error_modified = SPY['RV_d_pred_modified']-SPY['RV_d']
error_arr.append(sum(error_modified.dropna()**2))I’d call this an absolute success! The function is really smooth and the minimum is substatially lower than our standard models error.
So our optimal beta is 344.
Let’s look at the new models prediction:
That looks a lot better than our old model!
Time for an out of sample test on both.
We will train both models on the first half of the data set and train on the second half
Standard Model Error: 0.00048495452746367853
Modified Model Error: 0.0003485357222989575
Looks like our very easy modification to the model already captures the leverage effect quite well.
You can of course do this more optimally and fit the parameters in a better way but this is enough to show that it works.
Final Remarks
The files for this will be available on the discord as usual
Let me know what other papers you guys want to see in the future!










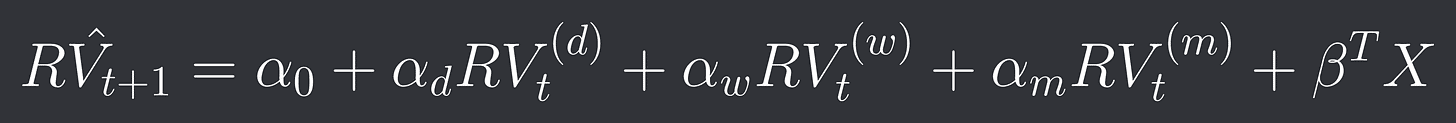









Hello Vertox, how do zou use this predictions in the strategy building pipeline? Do you use it for risk management, volatility trading or just as another predictor in some model ?