Statistical Arbitrage in the U.S. Equities Market (But in Crypto, with code, Part 3)

In this one we implement the paper in the title for the crypto market.

Paper: https://jeremywhittaker.com/wp-content/uploads/2021/03/AvellanedaLeeStatArb071108.pdf

In the last part we created a theoretical strategy. This part will be all about practicality.

---

Incorporating Mean First Passage Time

As a reminder, MFPT is the time your mean reverting process needs on average to return to the mean from some starting point. We’ve learned about this in the OU-Process Series.

Let us now look at the MFPT of the BTC residual:

mfpt = []

for entry in np.arange(0.01, 2.01, 0.01):
    mfpt_times = []
    
    long = False
    short = False

    cur_time = 0
    
    for i in range(len(residual['BTC'])):
        cur_time += 1

        if not long and norm_residual['BTC'].iloc[i] <= -entry:
            long = True
            cur_time = 0

        if not short and norm_residual['BTC'].iloc[i] >= entry:
            short = True
            cur_time = 0

        
        if long and norm_residual['BTC'].iloc[i] >= 0:
            long = False
            mfpt_times.append(cur_time)

        if short and norm_residual['BTC'].iloc[i] <= 0:
            short = False
            mfpt_times.append(cur_time)

    mfpt.append(np.mean(mfpt_times))

A little inaccurate, another problem of using daily data over higher frequency data, you have much much fewer data points. With let’s say hourly data you would have a nice line.

What we want to optimize for is profit per time. Profit here would just be our entry distance (unnormalized) and the time would be first the time each trade takes on average (MFPT) and the major one: the time it takes on average to wait for a trade. Let’s call this Mean First Reaching Time. (MFRT)

Here is what that looks like:

Now you can see why this is the major one, it grows exponentially which makes sense since our residual is mean reverting and further out datapoints become less and less likely.

Now let’s look at our optimization metric ((entry * residual_std)/(mfpt + mfrt)), I’m gonna call it profit per time:

Looks like our optimal entry is around the 1.25 std area.

Let us introduce 5bps of fees now and see how this changes:

As you can see now matter what we do now our returns are always negative. Why is that? It’s because we hedged way too much. We are actually hedging as much as possible using 13 assets which we actually shouldn’t do.
The more you hedge the more mean reverting your residual becomes but the smaller the variance becomes which makes it harder to beat fees. In addition the trade also becomes much harder to execute because you need to hit the right price on 13 assets.
We want’t to find a trade off between mean reversion, variance and ease of trading.

We will try 2 approaches for this:

1. Use our eigenvector weights as usual but only use the top n assets with the highest weight.

2. Create equally weighted or capitalization weighted sector groups of the top n assets in those sectors and hedge using those. For example Smart Contract Platform coins like ETH, BNB, ADA, SOL, TRX, etc. could form one portfolio.
   See https://www.coingecko.com/en/categories for more example.

---

Sparse Eigenvector Hedging

Let us first define the hedging vector which is just a weighted sum of all Q’s.

v_hedge = np.dot(betas, Q.T)

Notice anything? Whenever we were hedging a coin with a portfolio, that portfolio was basically just a short of this one coin with some tiny weights that you can’t even trade irl for the other coins. This obviously doesn’t make any sense. If we trade BTC then we don’t want exposure to BTC in our hedging portfolio.

Another thing I don’t really like about this approach is that it doesn’t make much economic sense. You always want to be able to explain *why* something you do should work. With the sector approach it makes perfect sense for assets in the same sector to behave similarly and to hedge each other out. Let’s therefore jump straight into method 2.

---

Sector Portfolios

Here are some example sector portfolios using 5 assets:

• Smart Contract Platform: ETH, BNB, ADA, SOL, TRX

• DEX Coins: UNI, CRV, CAKE, 1INCH, SUSHI

• CEX Coins: BNB, OKB, GT, KCS, HT

• Meme Coins: DOGE, SHIB, PEPE, FLOKI, BITCOIN

So if you wanted to trade UNI for example you would hedge with CRV, CAKE, 1INCH and SUHI.
I actually quite like that specific category because the coins are really similar so let’s get some HOURLY data for them.

UNI = pd.read_csv("UNIUSDT.csv").set_index('timestamp')["close"]
CRV = pd.read_csv("CRVUSDT.csv").set_index('timestamp')["close"]
CAKE = pd.read_csv("CAKEUSDT.csv").set_index('timestamp')["close"]
INCH = pd.read_csv("1INCHUSDT.csv").set_index('timestamp')["close"]
SUSHI = pd.read_csv("SUSHIUSDT.csv").set_index('timestamp')["close"]

dex = pd.concat([UNI, CRV, CAKE, INCH, SUSHI], axis=1)
dex.columns = ["UNI", "CRV", "CAKE", "INCH", "SUSHI"]
dex.dropna(inplace=True)
dex.reset_index(drop=True, inplace=True)

dex_rets = dex.pct_change(1).fillna(0)

Let’s regress the 4 DEX coins against UNI each 30 days (720 hours).

residual = []
coefs = []
i = 720
while i <= len(dex['UNI'])-720:
    dex_reg = LinearRegression()
    dex_reg.fit(dex_rets[['CRV', 'CAKE', 'INCH', 'SUSHI']].iloc[i-720:i], dex_rets['UNI'].iloc[i-720:i])

    coefs.append(dex_reg.coef_)
    residual.extend(np.cumprod(1 + dex_rets['UNI'].iloc[i:i+720]) - np.cumprod(1 + np.dot(coefs[-1], dex_rets[['CRV', 'CAKE', 'INCH', 'SUSHI']].iloc[i:i+720].T)))
    
    i += 720

Here is how they develop over time:

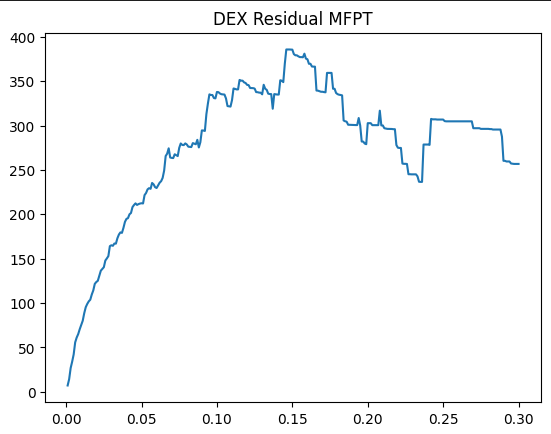
And here is what the residual looks like:

That’s what I call a nice looking residual!

Here is what longing at -0.05 and shorting at 0.05 looks like at 5bps of fees:

Let’s run our profit per time analysis on this:

The equity on this one portfolio alone is of course not amazing but the more portfolios you introduce the more consistent your returns become since there is some level of uncorrelation.

---

Final Remarks:

This is a very important lesson I had to learn as well, you shouldn’t keep looking for some amazing strategy with a straight up equity curve. Start running some strats live even if the equity isn’t amazing. You will learn the most that way and your different strategies will smooth out equity if they are uncorrelated.

That’s one of the goals I have with my substack, giving valuable ideas for some strategies that actually work so you can start doing what I just described. We’ve looked at momentum, seasonalities, mean reversion etc.
Just need to get the ball rolling.

Files will be available on discord as usual