Trading on Prediction Markets

Betting on Polymarket, Kalshi etc.

Prediction markets like Polymarket and Kalshi have been growing in popularity for a while now. They also provide bets on cryptocurrencies like “BTC price below $70000 on April 1st.”.
It is probably no surprise though that those markets are still greatly inefficient with lots of opportunities for us to make a profit.

For those types of bets one of the previous articles on simulating price paths comes in very handy:

We are gonna be using the techniques from that article to price the bets on prediction markets.

If you enjoy this article consider getting the paid subscription, that way you can support me and I can write even more articles!
Here is a discount code for those interested: https://www.vertoxquant.com/62375e34

---

Table of Content

1. An Overview of Prediction Markets

2. Pricing Bets

3. +EV bets

4. Market Making

5. Final Remarks

---

An Overview of Prediction Markets

Let’s start with the biggest prediction market, Polymarket (https://polymarket.com/).

We are primarily interested in 3 market categories:

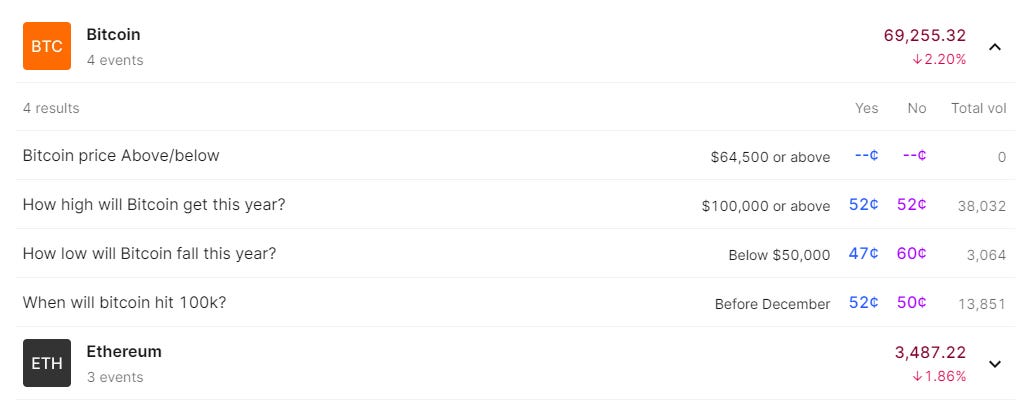
1. Crypto Prices

2. Bitcoin

3. Memecoins

If you can reliably simulate price paths then pricing things like “Will WIF hit $5 by April 30?” is super straightforward.

With Kalshi (https://kalshi.com/) we got a lot fewer markets available:

And the last one is Manifold (https://manifold.markets) where users can create their own bets:

I will only be focusing on Polymarket here though since that is the biggest and most liquid one.

---

Pricing Bets

Let’s start with the bet from earlier: “Will WIF hit $5 by April 30?”.

What we need to do to price this bet is:

1. Simulate a bunch of price paths starting now and ending April 30th 12pm.

2. Check the percentage of price paths that ever hit $5.

3. The fair price will be this percentage converted into cents.

I will be using hourly returns and fitting geometric brownian motion to them but you can of course use something more sophisticated, this is just to walk through how you would price those bets.

price = pd.read_csv("WIFUSDT-1h-data.csv").set_index("timestamp")
price.index = pd.to_datetime(price.index)
price = price.iloc[-100:]

rets = price['close'].pct_change(1).dropna()

Now let’s fit geometric brownian motion to this data:

mu = np.mean(rets)
sigma = np.std(rets)

N = 1000 # Number of price paths
T = 771 # Hours until bet is done

S0 = 3.945 # Current Price

paths = []
for i in range(N):
    path = [S0]
    for i in range(T):
        path.append(path[i] + mu*path[i] + sigma*path[i]*np.random.normal())

    paths.append(path)

paths = np.array(paths)

Now that’s not very realistic. That is a problem you will run into with geometric brownian motion, it will assume that price will keep going up at the same rate that it has historically. To be more conservative we can use simple brownian motion with a drift of 0.

Using those simulated price paths let us now calculate how many ever went above 5:

percentage = sum(np.any(paths >= 5, axis=1)) / len(paths)

Would I use this estimate to place bets though? No. The method used to simulate price paths here was way too inaccurate, I would have to pick a better model than that.
You can refer to the following post for other models:

There is also another way that you can price those bets: Using options data.
All those bets are some sort of binary option.

Options markets are obviously much more liquid and efficient than those betting markets and the prices will match the actual probabilities much more closely so you could use that data to construct a fair price and then use that to trade on betting markets, either buying / selling mispriced bets or market making around that fair price.

Let’s price another example using our simulated price paths.

“Ethereum above $3,500 on April 5?”
We once again simulate price paths until April 5th:

percentage = sum(paths[:,-1] > 3500) / len(paths)

---

+EV Bets

Consider the following scenario:
You think some event has a probability of 60% of happening and bid/ask are 40% and 50%.
You can imagine probabilities as prices, 40% corresponds to 40 cents and 50% to 50 cents. You therefore have the opportunity to buy something worth 60 cents for 50 cents.

There are 2 scenarios that could happen now:

1. You wait until the bet is over, if your probability is correct then you would make 50 cents 60% of the time and lose 50 cents 40% of the time. Clearly +EV.

   

2. Actual Price and your fair price cross. If your fair price stays 60 cents and the bid suddenly goes to 62 cents then you would obviously want to sell your bet for 62 cents.
   On the other hand if price doesn’t change but you suddenly think the probability is 30% then you would also want to sell your bet but now at 40 cents.

   If your probability was the correct one then the former is more likely to happen as price usually moves towards fair price.

Other than with fair value you can of course trade this in a more traditional way as well, although that could be challenging due to the high spreads. +EV opportunities will likely only appear during volatile times. Let’s say BTC suddenly drops by 5% but the bets for where the price of BTC will end up this week barely moved yet, this would be an opportunity to enter a mispriced bet.

Another +EV bet would be arbitrage, this could occur across different betting markets if they offer the same bet but also on the same market since you have a separate orderbook for yes and for no. You could for example buy Yes and sell No and construct an arbitrage that way if the prices don’t align.

---

Market Making

You have a few approaches to market making as well.
You could quote around the midprice or your own fair value that you got through for example Monte Carlo simulation like discussed above.

Another way would be to quote by keeping in mind the order book of the other outcome.
You would for example quote Yes at a price where if you get filled you can immediately place a market order on No and get an arbitrage.
With this sort of market-making you usually don’t need to worry about being left with market exposure for long periods of time. Of course it can happen that after you get filled the order on the other order book disappears and you can no longer construct an arb.
What market makers do in this case is either keep some inventory and adjust the other quotes to be more likely to decrease market exposure or they use market orders to get rid of their inventory at a loss.

---

Final Remarks

This was a pretty short post as I’m working on something big right now and didn’t have the time to work on another full-sized article, I hope you guys are fine with that!

You may have noticed that those betting markets are pretty similar to another market that we looked into in the past: the sports betting market.
Here is the article for those interested in it: