Honey, I Shrunk the Sample Betas
Why using raw betas will blow up your portfolio
Introduction
You build a clean, elegant beta-neutral portfolio.
Longs and shorts, carefully balanced, as all things should be.
Your regression says market beta is 0.02. Basically flat.
You go to sleep relaxed.
Then the market sells off 3%.
Your “beta-neutral” book is down 1.4%.
You can’t believe that happened.
You start digging:
Did correlations spike?
Was it exposure to another factor?
Is it all a conspiracy?
No.
The problem was already there before the sell-off even happened.
Your beta estimates were lying to you!
SOL doesn’t actually have a beta of 3.1; this just screams that it was estimated from noisy data.
But there’s a fix. A technique far more powerful than clamping beta estimates. One that shrinks your betas towards reality before they blow up your portfolio.
Why “Beta-neutral” Portfolios Aren’t Actually Neutral
Sample betas are just estimates. They’re noisy, unstable, and prone to exaggeration. The more extreme a beta looks, the more likely it’s lying.
The more aggressively you hedge with extreme betas, the more estimation error creeps in, and the less reliable your beta-neutral portfolio becomes.
Negative betas are especially dangerous. Imagine Asset A has a measured beta of 1.5 while Asset B has a measured beta of -1.5. You go long both, hoping to be beta-neutral. A few hours pass, and suddenly Asset B’s beta flips to 1.0, and your portfolio is suddenly long the market.
One thing many people do is clamp betas, which is not the right approach.
If you clamp betas at 2.0, then all your betas beyond that level just clump together at 2.0. There is suddenly no difference between a 2.1 and a 3.9 beta asset. Even within your capped group of assets, some positions are overweighted, some underweighted.
Statistically, clamping is crude because it introduces bias without reducing variance intelligently.
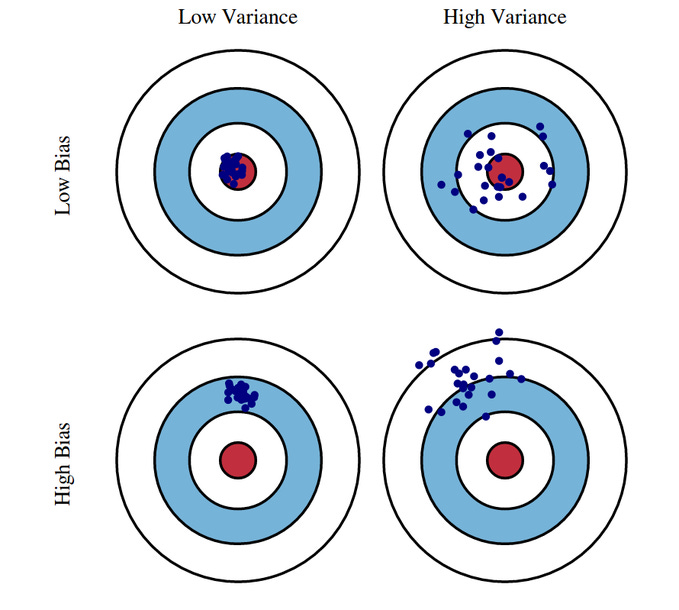
The Bias-Variance Tradeoff
In statistics and machine learning, every prediction faces a fundamental tradeoff: Bias vs Variance.
Bias is a systematic error: On average, your estimate is off.
Variance is the variability of your estimates across different samples.
Our goal now is to introduce some bias in order to reduce variance.
But why would we want to be wrong?!
Think of it like walking across a tightrope in a windstorm. You could try to react to every gust of wind, but if you misjudge once, you fall.
Or you can take a slightly biased, controlled path; You lean a little into the wind, and you make it across safely.
But instead of walking across a tightrope, you build a beta-neutral portfolio. And instead of falling, you lose the house.
Honey, I Shrunk the Betas
So how do we stop our “beta-neutral” portfolios from blowing up?
The answer is simple: shrink your betas.
Instead of trusting every extreme sample beta, we pull them toward a sensible center; usually 1 for market beta, or the average beta across your universe. If you want to be fancy, you could even group your assets by sector and shrink the betas within each sector to the average one.
Mild betas barely move, while extreme betas get pulled towards the center much more strongly.
In practice, the simplest form is linear shrinkage:
where
\hat{beta} = raw sample beta
beta_target = The center every beta gets pulled towards
w = How strong to pull.
w controls your bias-variance tradeoff. A smaller w leads to a lower variance, in exchange for higher bias. The longer the window is that you estimate betas on, the larger you typically want your w to be.
For those who like to go deeper, there are more advanced ways to shrink betas:
Bayesian shrinkage: Incorporate prior knowledge about beta distributions.
James-Stein: Learn the target from the cross-sectional distribution of all assets.
Conclusion
Raw beta estimates are noisy. Extreme betas are overconfident.
Trying to neutralize the market using raw beta estimates is a disaster waiting to happen.
Shrinkage is a smarter approach that pulls extreme estimates towards a reasonable center and keeps the portfolio’s relative structure intact.
It’s counterintuitive, but true: Sometimes being a little wrong on purpose makes you much more right when it matters.
So next time your regression spits out a 3.1 beta, don’t panic, don’t clamp it. Just shrink it.
If you wish for more practical Quant insights like this one, consider supporting us!
What you get:
Access to over 50 premium articles.
3 new premium articles per month.
Access to all the project code in the premium articles.
Access to the premium section of the Discord server.
Here you can have a taste of the premium articles:



Sorry. What does “SOL” refers to in the first paragraph?